In real life, resources are scarce and wants are unlimited. This fact leads us to optimize our resources to get best out of available resources. Our today’s post is related to Optimization. Optimization is a very vast topic to explore - we will learn how to do it with Excel 2010 optimization feature.

A formal definition:

Optimization is the action of making the best or most effective use of a situation or resource.

What is in this post?

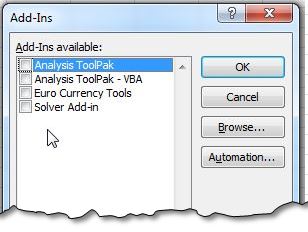
As has been our practice we will be taking up an example and will elaborate how to do it. Excel has a built in optimization tool called “Solver” that is used for this purpose. The Feature can be accessed by going to Data> Solver.

If the Option is not visible, you need to enable it first from the Files > Option > Add-Ins > Go > Solver to make it appear in the Data Tab.

Once done you are ready to go with the tools.

Our Problem:

This time, we are not looking to solve a resource allocation problem; rather, we are interested in solving a rather funny problem.

“We have rope of length 800 meters, what should be the length of the sides if we want to get maximum size of the rectangle?

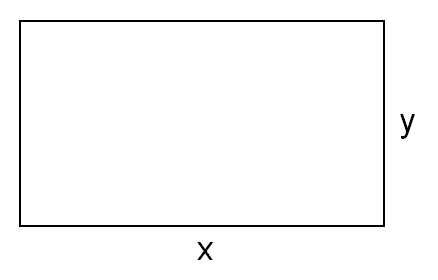
Now we will setup a sheet to use the Solver tool to solve for the value of x that will maximize the area of the rectangle.

Setting up Contraints and the problem in the solver

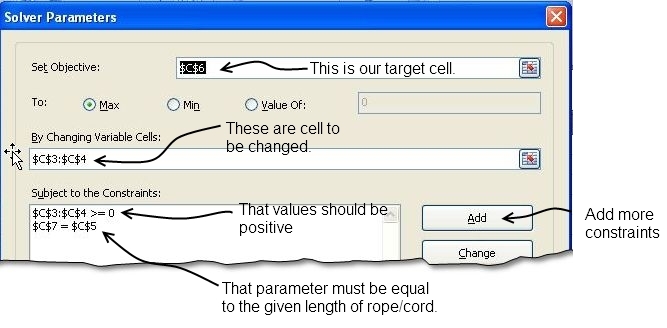
The target cell is the cell that should display our desired result – for our case it is $C$6. We will have changed values for x and y that is contained in the cell C3 and C4.

In order to get the appropriate and meaninful result, we will be adding two more conditions, one for non-nagetivity contraint and the other for length of cord/ rope being equal to the length of parimeter.

When we press ok, the solver comes up with a solution showing the length of the sides of the square and the resulting area.

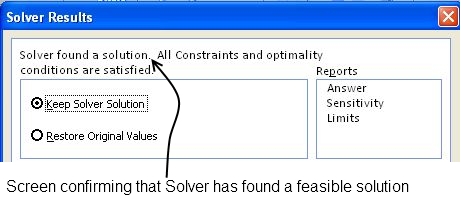
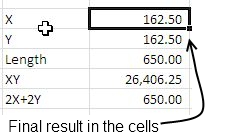
In some cases, Solver is not able to find the solution and will return the converse result. In such case you either need to adopt a better solver model or adjust your model by itself to get a correct solution. for this example, the length and width of 162.50 will give the maximum area.