Using Solver To Find The Most Profitable Mix Of Products

We came across such situation we have multiple choices and we want to find the best possible combination of them, be it spending money on shopping or adopting a route that is shortest or something else. The branch of mathematics that deals with such question is called Operations Research. As the desktop application has advanced with age of Computers, today we don’t have to perform these complicated calculation manually (they are taught in classrooms to explain the concept behind) but for computation purposes we use computer software.
One of such tools as available is Solver in MS Excel. MS Solver is a tool for optimization. It orders to access it, we have to install the analysis tool pack and after that it can be accessed from the Data Tab.
MS Solver allows us to setup multiple constrains to represent a situation and allows us to maximize, minimize or set something to value of, to solve the problem. When it comes to setting value to, it can be considered as a more advanced version of Goal Seek that optimizes only single variable to meet the requirements.
As usual we will explain the use of Solver with an example.
Example:
A production manager is interested in finding the best mix of products so that he can maximize the profit from factory operations. The fact sheet for the situation is below:
|
Profit/Unit |
Material A |
Material B |
Material C |
|
|
Product A |
12.50 |
1.00 |
2.50 |
1.30 |
|
Product B |
5.00 |
0.50 |
1.00 |
0.00 |
|
Product C |
20.00 |
2.00 |
1.50 |
2.00 |
|
Max Material Available |
- |
10,000.00 |
12,000.00 |
15,000.00 |
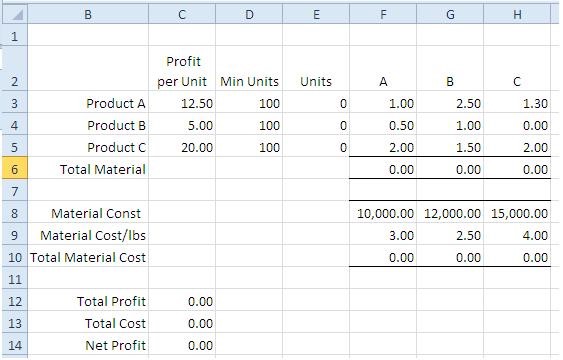 What is the best mix of products for this case?
What is the best mix of products for this case?
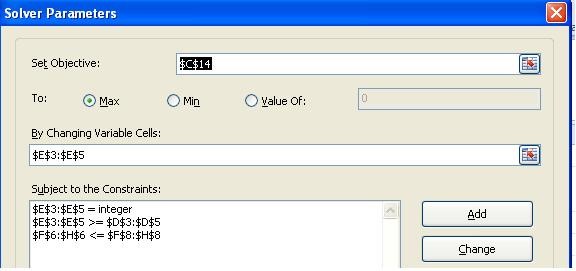
The fix starts by working out a sheet with all the relevant data and the constraints. See the following picture. With all this stuff setup we now have to setup the solver dialogue box.
We first start by setting the target cell. That is for this case is the C14 that shows Net Profit that is calculated by taking the difference of Total Profit less Total Cost.
With this we have selected the option of maximize i.e. we want to maximize the profit.
Now we start adding the constraints i.e. the limitations we face with this situation. Consider following:
- Setting a lower limit for Units to be produced i.e. minimum number of units to be produced
- We have limited supply of raw material, hence a constraint that material be used should always be less then or equal to the total raw material.
- That Product should always be in integers (we can’t produce 2.5 units of a soap or cold drink cane).
With these three constrains in effect, the final dialogue box looks like this:
And on pressing OK, the solver successfully gives us a solution:
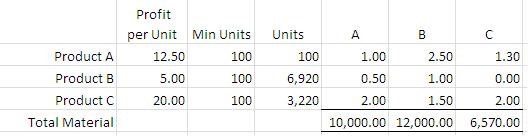
You can see from the result that Product A has only marginal effect on the total profit hence only 100 units are to be produced. For practical purposes you can simply ignore such variables and go forward with Product B and C only.
Thus with few click you can have a solution that is other very tedious task to achieve.











